Minimize Travel Tax :
Difficulty Level : Hard
Submissions : 434
Asked In :
Marks :20
: 14 | : 1
There are $$$n$$$ cities connected by $$$n-1$$$ bi-directional roads such that all the cities are connected.
You go on $$$m$$$ trips where on the $$$i-th$$$ trip you travel from city $$$u_i$$$ to city $$$v_i$$$. All the trips are independent of each other. You have to pay a tax of $$$tax_i$$$ on entering or leaving the $$$i-th$$$ city. If you pay the tax while entering then you don't need to pay at the time of leaving.
You can choose some non-adjacent cities and make their tax half. What can be the minimum sum of taxes you pay for all the $$$m$$$ trips?
The first line contains a single integer $$$t$$$ $$$(1 \leq t \leq 10^4)$$$ — the number of test cases. The description of $$$t$$$ testcase follows.
The first line of each testcase contains two integers $$$n$$$ and $$$m$$$ $$$(1 \le n,m \le 10^5)$$$ — the number of nodes and the number of trips. The nodes are numbered $$$1,2,…,n$$$.
The second line contains $$$n$$$ space separated integers $$$tax_1,tax_2,...tax_n$$$ $$$(2 \le tax_i \le 10^9; \hspace{2 pt} tax_i\%2 == 0)$$$ denoting the taxes at the nodes of the tree.
The next $$$n-1$$$ lines describe the tree. Each contains two space separated integers $$$u$$$ and $$$v$$$ $$$(1 \le u, v \le n; u \neq v \hspace{1 pt})$$$ denoting an edge between vertices $$$u$$$ and $$$v$$$. It is guaranteed that these edges form a tree.
Finally, there are $$$m$$$ lines describing the trips. Each line contains two integers $$$u$$$ and $$$v$$$ $$$(1 \le u, v \le n; u \neq v \hspace{1 pt})$$$ denoting a trip from city to $$$u$$$ to city $$$v$$$.
It is guaranteed that the sum of $$$n$$$ and $$$m$$$ over all test cases does not exceed $$$10^5$$$ each.
For each testcase, print a single integer — the minimum sum of taxes you pay for all the trips in a single line.
2 3 2 2 2 8 1 2 1 3 1 3 3 2 3 2 2 4 2 1 2 2 3 1 3 1 2
13 10
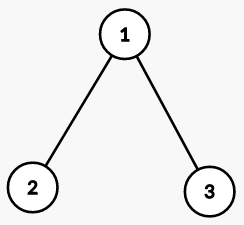Sample test case 1- For trip 1, from 1 to 3: you will have to pay taxes at cities 1 and 3.
- For trip 2, from 3 to 2: you will have to pay taxes at cities 1,2 and 3.
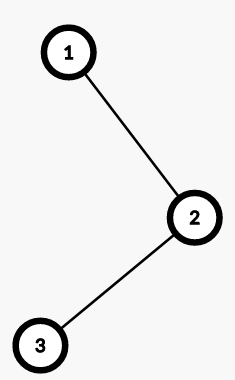Sample test case 2- For trip 1, from 1 to 3: you will have to pay taxes at cities 1, 2 and 3.
- For trip 2, from 1 to 2: you will have to pay taxes at cities 1 and 2.
